Special relativity

We will not use the same formulation of special relativity as Einstein did in 1905 []; instead we adopt Minkowski's presentation from 1907 (see e.g. [], [], []). Minkowski's approach consists of a geometrization, which was not well received by Einstein until he realized that it was necessary for the theory to be generalized. In contrast to Newtonian theory, space and time are according to relativity bound together into a continuum called space-time, where the flow of time and length of objects are dependent on in which frame they are measured. Throughout the rest of this thesis we use conventions \[ c = G = \epsilon_0 = \mu_0 = \hbar = k = 1, \] where $G$ is still the Newtonian constant of gravitation, $c$ is the speed of light, $\epsilon_0$ the dielectric constant or static permittivity, $\mu_0$ the vacuum permeability, $\hbar$ Planck's constant, divided by $2 \pi$, and $k$ Boltzmann's constant.

The Minkowski space-time

Minkowski realized in 1907 that Einstein's special relativity could be described in terms of a four-dimensional space-time, where the three (Euclidean) space dimensions are merged with one time dimension. Or in his own words:

"The views of space and time which I wish to lay before you have sprung from the soil of experimental physics, and therein lies their strength. They are radical. Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality."
-Hermann Minkowski

The Minkowski geometry is a space-time that is flat, i.e. curvature free, and described by $\left ( \mathbb{R}^4, \eta \right )$, where $\eta$ is a flat metric with Lorentzian signature. In flat space-time there exists preferred coordinates analogous to Cartesian coordinates in Euclidean space. Written in such coordinates the components of $\eta$ take the form \begin{equation}\label{Minkowski-metric} \eta _{\mu \nu} = \left( {\begin{array}{*{20}c} { - 1} & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array}} \right) = diag \left [ -1,1,1,1 \right ]. \end{equation}

The Minkowski line element

If one use Cartesian coordinates one can describe Euclidean geometry with the line element $ds^2 = dx^2 + dy^2 + dz^2$, which describes the infinitesimal distance between two nearby points. In the case of Minkowski space-time one instead has four coordinates $(t,x,y,z) = (x^0, x^1, x^2, x^3)$ and a line element that takes the form \[ ds^2 = - dt^2 + dx^2 + dy^2 + dz^2, \] which, by means of the Minkowski metric (\ref{Minkowski-metric}), can be written as \begin{equation}\label{linjeelement} ds^2 = \eta _{\mu \nu} dx^\mu dx^\nu, \end{equation} where we have used Einstein's summation convention¹ of using sums over repeated indices in order to make expressions less cluttered. Here the similarity with Euclidean geometry is rather obvious, the only new thing that is different is the $- dt^2$ term, but this yields some new features. Now $ds^2$ can still be positive or zero, just as one is used to, but it is sometimes negative and there is a new way to get a zero line element.

$ds^2 < 0$: This corresponds to $dt^2 > dx^2 + dy^2 + dz^2$. In this case the space-time interval $ds^2$ is said to be timelike.
$ds^2 = 0$: This corresponds to two different situations:
1. $dx ^\mu = 0$, and $ds^2$ is zero.
2. $dt^2 = dx^2 + dy^2 + dz^2 \neq 0$; here the distance is the same in time as it is in space, but $ds^2$ is still zero and one says that it represents a null interval.
$ds^2 > 0$: This corresponds to $dt^2 < dx^2 + dy^2 + dz^2$; the space-time interval $ds^2$ is said to be spacelike.

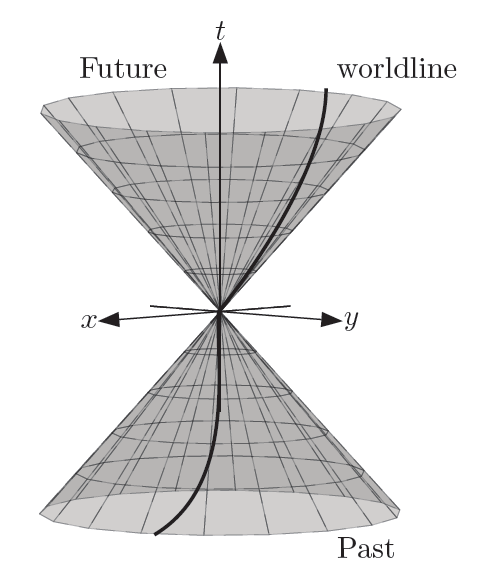
Space-time diagrams

In a space-time diagram the convention is that time is directed upwards in the diagram, while one or two spatial axes are positioned in the horizontal plane. There are several useful concepts which can be visualized in space-time diagrams.

Events: Points in the space-time diagram are known as events.
Worldline: The line that shows the position of a point-like material object as a function of time is known as a worldline, see Figure \ref{Fig:cone}. The tangent of the worldline at an event determines the four-velocity of the particle at this event.
Light cone: Plotting events that are related via null intervals in two space and one time dimension, results in a light cone with two parts, one future and one past of the event that connects the two, see Figure \ref{Fig:cone}.

$Light cone$

Lorentz transformations

One important property of $ds^2 = \eta_{\mu \nu} dx^\mu dx^\nu$ is that during a so-called Lorentz transformation $ds^2$ will not change its form, even though each $d x^\mu$ may change; one thus have \[ \eta _{\mu ' \nu '} dx^{\mu '} dx^{\nu '} = \eta _{\mu \nu} dx^\mu dx^\nu, \] where $\eta _{\mu \nu} = diag \left [ -1,1,1,1 \right ] = \eta _{\mu ' \nu '}$. One important example of a Lorentz transformation is a so-called boost. In special relativity every event can be described by four Minkowskian coordinates, one time and three space coordinates, that jointly form an inertial frame $R$, but in a boosted Minkowskian reference frame $R'$, i.e. a frame that moves with constant speed $v$ in e.g. $R$'s $x$ direction, one obtains the following \begin{equation}\label{Lorentz} \left\{ \begin{array}{l} t' = \gamma \left( {t - vx} \right) \\ x' = \gamma \left( {x - vt} \right) \\ y' = y \\ z' = z \\ \end{array} \right. , \end{equation} where $\gamma$ is known as the Lorentz factor or $\gamma$-function, given by \[ \gamma = \frac{1}{{\sqrt {1 - v^2 } }}; \] since $0 \le v < 1$, it follows that $\gamma > 1$. A more modern way of writing (\ref{Lorentz}) is as follows. Let $(t,x,y,z) = (x^0, x^1, x^2, x^3)$ and introduce the transformation matrix \[ \Lambda ^{\mu '} _{\ \nu} = \left( {\begin{array}{*{20}c} \gamma & { - v\gamma } & 0 & 0 \\ { - v\gamma } & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array}} \right), \] then the boost transformation takes the form \begin{equation}\label{boost} \begin{aligned} x^{\mu '} = & \left( {\begin{array}{*{20}c} {t'} \\ {x'} \\ {y'} \\ {z'} \\ \end{array}} \right) = \Lambda ^{\mu '}_{\ \nu} x^\nu = \\ = & \left( {\begin{array}{*{20}c} \gamma & { - v\gamma } & 0 & 0 \\ { - v\gamma } & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array}} \right) \left( {\begin{array}{*{20}c} t \\ x \\ y \\ z \\ \end{array}} \right) = \left( {\begin{array}{*{20}c} {\gamma t - \gamma vx} \\ {\gamma x - \gamma vt} \\ y \\ z \\ \end{array}} \right). \end{aligned} \end{equation} Here the Einstein summation convention has been used, and one easily sees that the result is exactly the same as in (\ref{Lorentz}).

Addition of velocities

When students first learn how to add different velocities in the same direction they use ordinary vector addition in 3-dimensional Euclidean space, which leads to the result that one merely adds the two speeds: \[ V = v_1 + v_2. \] But in special relativity the addition of speeds is not so simple; instead \[ V = \frac{v_1 + v_2 }{1 + v_1 \cdot v_2 }. \] In the limit where $v_1, v_2 \ll 1$ one will not notice much of a difference; if one chooses $v_1, v_2 = 0.01$ then $v_{Newton} = 0.02$ and $v_{Einstein} = 0.0196$, a difference of $2 \%$, and in the fully relativistic limit, where one of the velocities is the velocity of light, one gets, \[ v_{Einstein} = \frac{1 + v }{1 + v} = 1, \] a result that is independent of one's own speed or frame. The Newtonian addition law yields \[ v_{Newton} = 1 + v, \] and hence there is a $v \%$ difference.

Simultaneity

By differentiating (\ref{Lorentz}) one gets \[ \Delta t' = \gamma \left( {\Delta t - v\Delta x} \right). \] If two events are simultaneous $\left( \Delta t = 0 \right)$ in a frame $R$, then they are in general not simultaneous in the frame $R'$, since it is then required that they are co-local $\left( \Delta x = 0 \right)$.

Time dilation and length contraction

If there in the frame $R$ is a stationary $\left( \Delta x = 0 \right)$ clock and the difference between two ticks is constant with $\Delta t$ fixed, when described from the frame $R$, in the frame $R'$ the separation between two ticks will be \[ \Delta t' = \gamma \Delta t. \] Thus the time difference in $R'$ will always be greater then in $R$ as seen from $R'$, in other words, time moves slower in $R'$. This is the effect known as time dilation. If one instead chooses a rod with the length $\Delta x$, and fix synchronized clocks at each end of the rod s.t. they are simultaneous in $R$, i.e. $\Delta t = 0$, then this leads to \[ \Delta x' = \frac{\Delta x}{\gamma }. \] Thus, when viewed from $R$, a moving rod in $R'$ is shorter than it is when being stationary, an effect known as length contraction.

Proper time

A clock that travels on a timelike path $T$ between two non co-local events will measure the proper time, $\tau$, between these events, which is given by \[ \tau = \int d\tau, \] where \begin{equation}\label{propertime} d\tau = \sqrt {- \eta _{\mu \nu } dx^\mu dx^\nu }, \end{equation} and where the integral is taken over the woldline $T$.

Velocity, acceleration, momentum and force in 4D

The tangent vector along a timelike worldline $x^\mu (\tau)$ is the four velocity, $U ^\mu$, given by \begin{equation}\label{fourvel} U ^\mu = \frac{dx ^\mu}{d \tau}. \end{equation} It follows from (\ref{propertime}) that $U ^\mu$ is automatically normalized \[ \eta _{\mu \nu} U ^\mu U ^\nu = -1. \] The four-acceleration is defined as, \[ a^\mu = \frac{d U ^\mu}{d \tau}, \] while the four-momentum of a point particle traveling along a worldline with four-velocity, $U^\mu$, is defined as \[ p ^\mu = mU ^\mu, \] where $m$ is the rest mass of the point particle, and where the rest mass is a Lorentz invariant and thus independent of which frame is being used. The time component, $p^0$, is the particle's energy. In its rest frame (the frame where speed of the particle is zero), $p^0 = m$, which in the units being used here might not look spectacular, but recall that we use the convention $c = 1$. If we refrain from setting $c = 1$ we obtain \[ p^0 = E = mc^2, \] which is the most well known formula in all of physics. The four-force is defined as the rate of change of $p^\mu$ w.r.t. proper time $\tau$, i.e., \[ F^\mu = \frac{d p^\mu}{d \tau} = m\frac{d U^\mu}{d \tau} = m a^\mu. \]

1. ^ $ds^2 = \eta _{\mu \nu} dx^\mu dx^\nu$ is short for $ds^2 = \sum\limits_{\mu, \nu = 0}^3 {\eta _{\mu \nu} dx^\mu dx^\nu}$.